Claude Shannon

Early Years

• Born in Petosky, Michigan
• Grew up in Gaylord, Michigan
• Mother was a high school principal
• Father was a Probate Judge

Early Years

• Early aptitude for mathematics and science
• Built various devices as a youth
• Model planes
• Radio-controlled boat
• Telegraph system to a friend's house with the wire fencing
• Distant cousin to Thomas Edison

Boolean algebra applied in circuits

• After graduation, begins studying electrical engineering at MIT in 1936
  • Worked under Vannevar Bush with analog differential analyzers
  • Took a course from Norbert Weiner
  • Spent the summer of 1937 at Bell Labs, influenced later work

Boolean algebra applied in circuits

• Works on early analog computers and designs switching circuits based on Boolean logic
  • At first applied to simplify telephone switching relays
  • Then proven that all Boolean algebra problems can be solved via circuits
  • Foundation for all electronic digital computers

Boolean algebra applied in circuits

• Published Master’s thesis in 1937 based on this work
  • A Symbolic Analysis of Relay and Switching Circuits
  • Has been called “one of the most important master’s theses ever written”
  • 22 years old

Doctorate and Institute for Advanced Study

• Completed his doctoral degree from MIT in 1940
  • Dissertation: An Algebra for Theoretical Genetics
  • Application of mathematics to genetics
    • Completed in less than a year
  • Also spent time in a flight training program

Doctorate and Institute for Advanced Study

• National Research Fellow at the Institute for Advanced Study for the year following
  • This place should sound familiar by now.
  • Worked under mathematician Herman Weyl, interacted with:
    • John von Neumann: “He was the smartest person I ever met”
    • Kurt Gödel
    • Albert Einstein

Doctorate and Institute for Advanced Study

Side story:

"Einstein once showed up for one of Shannon’s lectures, but was apparently looking for the tea room and left.”

Bell Labs

• Understands that he wants to solve problems related to the transmission of information
• Returns to Bell Labs in summer of 1941
• One small event prevents from focusing on his interests: World War II

Bell Labs

• To help the war effort, Shannon works under the National Defense Research Committee
  • NDRC established by FDR and headed by Vannevar Bush
  • Works under Hendrik Bode to develop “software” for fire control systems
    • Heavily influenced by previous work of Norbert Weiner
    • Saw analogy between removing interference in communication signals and errors in tracking signals

Bell Labs

• Also works in cryptography at Bell Labs
• Asked to inspect the encryption of a secure digital communication system, X System or SIGSALY
  • Used for secure communications between the United States and the UK during WWII
  • Interactions were restricted, but he met a mathematician by the name Alan Turing
    • Turing came to Bell Labs in January 1943 and stayed for 2 months
    • Spoke about common interests outside of work
    • Shannon said he received “a fair amount of negative feedback”

A Mathematical Theory of Cryptography

• Classified report by Shannon which was published in 1945
• Applied probability theory to cryptography
  • Rigorously used mathematics to prove aspects of cryptography, like how a random one-time pad encryption scheme is unbreakable
  • The declassified version of this report was released in 1949 under the title Communication Theory of Secrecy Systems

A Mathematical Theory of Cryptography

• Much of the concepts introduced would be later used in his later work on information theory
  • One footnote of this paper literally announces the future work:

“It is intended to develop these results in a coherent fashion in a forthcoming memorandum on the transmission of information.

A Mathematical Theory of Communication

• Shannon’s seminal work (at least in his opinion) which was published in 1948
• Work with information theory was unofficial, unlike with fire control systems and cryptography
  • Most ideas were developed from 1943 to 1945, but delayed due to the war
  • War also helped though, through his time spent with cryptography

A Mathematical Theory of Communication

• A start for Shannon’s idea came from “Hartley’s paper”
  • Ralph Hartley was a Bell Labs researcher, published Transmission of Information in 1925
  • Attempted to quantitatively measure the transmission of information
• Nyquist’s work on sampling and bandwidth of transmission mediums also greatly impacted Shannon

A Mathematical Theory of Communication

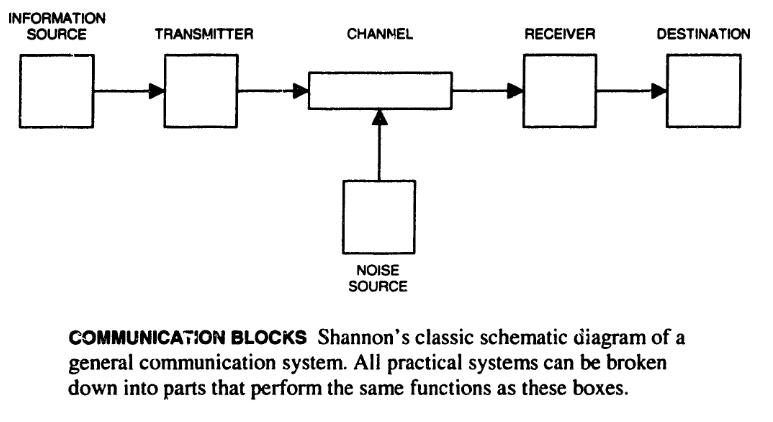
A Mathematical Theory of Communication

• At the time, communications remained split:
  • Military kept radar under a cloak of secrecy
  • AT&T was the sole operator of the telephone system
  • Universities primarily focused on radio transmissions
• Shannon’s worked unified many various fields by laying a mathematical foundation irrespective of any particular system or technology

A Mathematical Theory of Communication

• Fundamental unit of information: a “bit”
  • At one lunch, researchers were searching for a term for “binary digit”
  • John Tukey said the “best and obvious choice” was the term bit
• Shannon viewed information as a measure of uncertainty

A Mathematical Theory of Communication

• We want to view things that are unknown to us, so we learn about them
• Communication then becomes the resolution of uncertainty
• Using his sampling theory derived from Nyquist’s work, any continuous signal can be discretized and turned into a digital one

A Mathematical Theory of Communication

• Once digital, any message can then be encoded in variety of ways
  • Same number of bits for each symbol
  • Varying amount of bits per symbol
  • Varying amount of bits per combinations of symbols

A Mathematical Theory of Communication

• We can analyze the frequency of certain combinations of symbols to compress the transmission
• Then leads to the question: How much compression is possible?
• Shannon’s measure of information tells us how many bits are required to efficiently encode information

A Mathematical Theory of Communication

• Analysis of the structure of a source allows for more efficient encoding by removing redundancy
• This all equals more cat videos

A Mathematical Theory of Communication

• Back to redundancy, Shannon showed that adding redundancy allowed for the suppression and correction of errors in the transmission of messages
• However, redundancy can introduced more intelligently than just repeating the message
  • See the work of Richard Hamming and Hamming codes

A Mathematical Theory of Communication

• This paper proves an upper limit for transmitting data for every method of communication
  • Maximum amount of bits per second
• Shannon combined the ideas of Hartley and Nyquist, relating bandwidth and error rates, to give a mathematical definition for the capacity of a given channel

A Mathematical Theory of Communication

• Furthermore, he proved that any method of transmission could be done at capacity and be error-free
  • The catch is that he only proved they exist, not how to actually get them

Aftermath

• At 32 years old, Shannon garnered interest from around the world with his work
  • Not all was positive though
    • Mathematician Joseph Doob argued that the proofs were not rigorous enough
• Paper was successful due to the pragmatic focus that Shannon had with a background in both mathematics and electrical engineering

Aftermath

• Ultimately, the entirety of A Mathematical Theory of Communication was proven to be correct
• After meeting in 1948, Shannon marries Mary Elizabeth “Betty” Moore in March of 1949
  • Betty was a mathematician in her own right at Bell Labs, and would often help Shannon with his idea
  • Also, Shannon hated to write and Betty would help dictate in addition to helping Shannon formulate his thoughts

Back to MIT

• After 15 years with Bell Labs, Shannon leaves in 1956
• Returns to MIT in order to maintain the intellectual freedom to pursue his interests
• He began teaching advanced courses in information theory, and MIT became a leading institution in the field
• His personality lead him to avoid much teaching or advising, but he continued pursuing problems

Back to MIT

• Contributed to work in Artificial Intelligence
  • Supervised Marvin Minsky and John McCarthy during summer lab jobs, both of whom are pioneers in A.I.
• Advised Leonard Kleinrock and Ivan Sutherland who would go on to work with the Internet and computer graphics respectively

More about his personal life

• His love of devices continued past his youth
  • Wrote about machines playing chess
  • Created a mechanical “mouse” that could solve a maze, part of his work in A.I.
  • Collaborated to created a machine for card counting then test
  • Tried to build a machine to solve a Rubik’s cube
  • A calculator that used Roman numerals

More about his personal life

• In 1951, Betty gave Shannon a unicycle, which he rode in the hallways at Bell Labs
• Shannon was also an avid juggler which, in tandem with a unicycle, clearly helped him to focus
• Allegedly had a trumpet that would shoot fire

Later years

• Shannon officially retired from MIT in 1978
  • By many accounts, he had already retired from teaching, preferring his own interests
• Applied mathematics to juggling and published a juggling theorem
  • Went up to the juggling club at MIT and asked if he could measure them
  • Soon after, invited them over to watch juggling videos, play with his devices, and eat pizza

• Did well financially by investing in tech companies founded by friends
  • Teledyne
  • Codex
  • Hewlett-Packard

• Sometime within the early 1990’s, Shannon developed Alzheimer’s disease

“He vaguely remembered I juggled, and cheerfully showed me the juggling displays in his toy room, as if for the first time. And despite the loss of memory and reason, he was every bit as warm, friendly, and cheerful as the first time I met him.”

• After spending a few years in a nursing home, Shannon passed away on February 24th, 2001, at the age of 84
• His wife said “He would have been bemused” by the digital world he helped to create